数据结构
1 线性数据结构
1.1 数组
1.2 链表
1.3 栈
1.4 队列
2 图
2.1 基本概念
2.2 图的存储
2.3 图的搜索
2.3.1 DFS
public int[] findOrder(int numCourses, int[][] prerequisites) {
// adjacency list
Set<Integer>[] graph = new Set[numCourses];
for (int[] e : prerequisites) {
// e[0] depends on e[1]
// e[1] --> e[0]
if (graph[e[1]] == null) {
graph[e[1]] = new HashSet<>();
}
graph[e[1]].add(e[0]);
}
List<Integer> list = new ArrayList<>(numCourses);
boolean[] globalVisited = new boolean[numCourses];
boolean[] localVisited = new boolean[numCourses]; // to check cycle
for (int i = 0; i < numCourses; ++i) {
if (!dfs(graph, i, globalVisited, localVisited, list)) {
return new int[0];
}
}
// copy and reverse
int[] result = new int[numCourses];
for (int i = 0; i < numCourses; ++i) {
result[i] = list.get(numCourses - i - 1);
}
return result;
}
// return: can finish
public boolean dfs(Set<Integer>[] graph, int node, boolean[] globalVisited, boolean[] localVisited, List<Integer> list) {
if (localVisited[node]) return false;
if (globalVisited[node]) return true;
localVisited[node] = true;
globalVisited[node] = true;
Set<Integer> next = graph[node];
if (next != null) {
for (Integer n : next) {
if (!dfs(graph, n, globalVisited, localVisited, list)) {
// return false and exit, no need to reset localVisited
return false;
}
}
}
localVisited[node] = false; // reset
list.add(node);
return true;
}
2.4 图的路径
2.4.1 弗洛伊德
class Solution {
public int networkDelayTime(int[][] times, int N, int K) {
// w[i][j]: time from [i] to [j], Integer.MAX_VALUE: inf
int[][] w = new int[N+1][N+1];
for (int i = 1; i <= N; ++i) {
Arrays.fill(w[i], Integer.MAX_VALUE);
w[i][i] = 0;
}
for (int[] e : times) {
int u = e[0], v = e[1], t = e[2];
w[u][v] = t;
}
for (int k = 1; k <= N; ++k) {
for (int i = 1; i <= N; ++i) {
for (int j = 1; j <= N; ++j) {
int sum;
if (w[i][k] == Integer.MAX_VALUE w[k][j] == Integer.MAX_VALUE) {
sum = Integer.MAX_VALUE;
} else {
sum = w[i][k] + w[k][j];
}
w[i][j] = Math.min(w[i][j], sum);
}
}
}
int max = -1;
for (int j = 1; j <= N; ++j) {
if (w[K][j] == Integer.MAX_VALUE) return -1;
max = Math.max(max, w[K][j]);
}
return max;
}
}
2.4.2 Dijkstra
class Solution {
public int networkDelayTime(int[][] times, int N, int K) {
// graph[i]: List<int[]>, [to node, w]
List<int[]>[] graph = new List[N+1];
for (int i = 1; i <= N; ++i) {
graph[i] = new LinkedList<>();
}
for (int[] e : times) {
int from = e[0], to = e[1], w = e[2];
graph[from].add(new int[]{to, w});
}
// [distance, node]
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> a[0] - b[0]);
// node --> min distance
HashMap<Integer, Integer> dist = new HashMap<>();
heap.offer(new int[]{0, K});
while (heap.size() > 0) {
int[] n = heap.poll();
int distance = n[0];
int node = n[1];
if (dist.containsKey(node)) continue; // already determined
dist.put(node, distance); // node determined
for (int[] g : graph[node]) {
int nextNode = g[0];
int w = g[1];
// K --> ... --> node --> nextNode
if (dist.containsKey(nextNode)) continue; // alreay determined
heap.offer(new int[]{distance + w, nextNode});
}
}
if (dist.size() != N) return -1;
int max = -1;
for (int d : dist.values()) {
max = Math.max(max, d);
}
return max;
}
}
2.5 图的出入度问题
class Solution {
public int[] findOrder(int numCourses, int[][] prerequisites) {
Map<Integer, List<Integer>> graph = new HashMap<>();
int[] indegree = new int[numCourses];
for (int[] e : prerequisites) {
// e[0] depends on e[1]
// e[1] --> e[0]
int pre = e[1], cur = e[0];
List<Integer> list = graph.get(pre);
if (list == null) {
list = new LinkedList<>();
graph.put(pre, list);
}
list.add(cur);
indegree[cur]++;
}
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < numCourses; ++i) {
if (indegree[i] == 0) {
queue.add(i);
}
}
int[] result = new int[numCourses];
int size = 0;
while (queue.size() > 0) {
int node = queue.poll();
result[size++] = node;
List<Integer> next = graph.get(node);
if (next != null) {
for (int n : next) {
indegree[n]--;
if (indegree[n] == 0) {
queue.offer(n);
}
}
}
}
if (size != numCourses) return new int[0];
return result;
}
}
2.6 最小生成树
2.6.1 Kruskal
class Solution {
public int minimumCost(int N, int[][] connections) {
// sort connections by cost from small to large
Arrays.sort(connections, (a,b) -> a[2]-b[2]);
int[] parent = new int[N+1];
for (int i = 1; i <= N; ++i) {
parent[i] = i;
}
int cost = 0;
for (int[] edge : connections) {
if (union(edge[0], edge[1], parent)) {
cost += edge[2];
}
}
// check if all the roots are the same
int p = -1;
for (int i = 1; i <= N; ++i) {
int root = findRoot(i, parent);
if (p == -1) {
p = root;
} else if (p != root) {
return -1;
}
}
return cost;
}
public int findRoot(int x, int[] parent) {
while (x != parent[x]) {
parent[x] = parent[parent[x]];
x = parent[x];
}
return x;
}
public boolean union(int a, int b, int[] parent) {
a = findRoot(a, parent);
b = findRoot(b, parent);
if (a == b) return false;
parent[a] = b;
return true;
}
}
2.6.2 Prim
class Solution {
public int minimumCost(int N, int[][] connections) {
int INF = Integer.MAX_VALUE;
// graph[i][j]:
// INF: not reachable
// x: distance
int[][] graph = new int[N+1][N+1];
for (int i = 1; i <= N; ++i) {
for (int j = 1; j <= N; ++j) {
if (i == j) graph[i][j] = 0;
else graph[i][j] = INF;
}
}
for (int[] edge : connections) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u][v] = graph[v][u] = w;
}
// dist[i]
// d: current min distance from one of added nodes
// INF: distance is inf, not reachable
int[] dist = new int[N+1];
Arrays.fill(dist, INF);
// added nodes
boolean[] added = new boolean[N+1];
// set node [1] as candidates
dist[1] = 0;
int cost = 0;
for (int k = 0; k < N; ++k) { // N nodes to add
// find node with min distance
int min = INF;
int node = -1;
for (int i = 1; i <= N; ++i) {
if (!added[i] && dist[i] < min) {
min = dist[i];
node = i;
}
}
// no reachable node found
if (node == -1) {
return -1;
}
// add [node]
cost += dist[node];
added[node] = true;
// update dist[i] with distance from [node] to [i]
for (int i = 1; i <= N; ++i) {
if (added[i]) continue;
if (graph[node][i] == INF) continue;
dist[i] = Math.min(dist[i], graph[node][i]);
}
}
return cost;
}
}
3 堆
3.1 概念
3.2 分类
3.3 存储
3.4 操作
3.5 排序
4 树
4.1 分类
4.2 存储
4.3 遍历
5 红黑树
5.1 概念与特点
红黑树是一种自平衡二叉查找树。JDK中,TreeMap、TreeSet以及HashMap都使用了红黑树。
特点:
- 节点非黑即红,黑色决定平衡,红色不决定平衡。
- 根节点总是黑色的。
- 每个叶子节点都是黑色的空节点。
- 如果节点是红色,那它的子节点一定是黑色(反之不一定),胡总和说不会有连续的红色节点。一个节点最多临时有三个节点,中间黑,左右红。
- 从任意节点到他的叶子节点或空子节点的每条路径,必定包含相同数量的而黑色节点。每一层都只有一个节点贡献了树高决定平衡性,也就是对应红黑树中的黑色节点。
红黑树高度不会超过2log(n+1)
5.2 数据结构
建立在 BST 二叉搜索树的基础上,AVL、2-3 树、红黑树都是自平衡二叉树(统称 B-树)。但相比于 AVL 树,高度平衡所带来的时间复杂度,红黑树对平衡的控制要宽松一些,红黑树只需要保证黑色节点平衡即可。
public class Node {
public Class<?> clazz;
public Integer value;
public Node parent;
public Node left;
public Node right;
// AVL 树所需属性
public int height;
// 红黑树所需属性
public Color color = Color.RED;
}
5.3 平衡调整
- 左倾染色
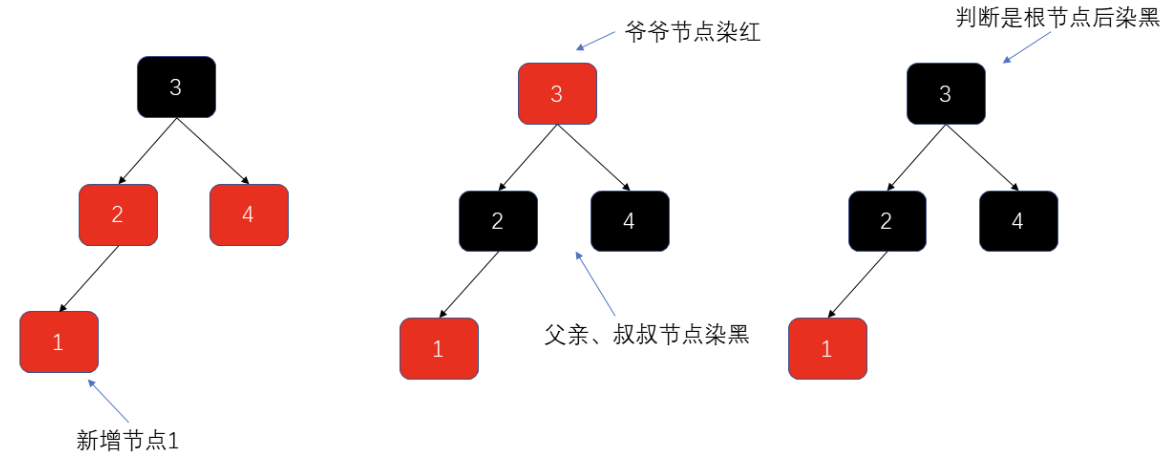
- 染色时根据当前节点的爷爷节点,找到当前节点的父亲、叔叔节点
- 把父亲、叔叔节点染黑,爷爷节点染红。
- 爷爷节点染红是临时的,当平衡树高操作后,会把根节点染黑
- 右倾染色
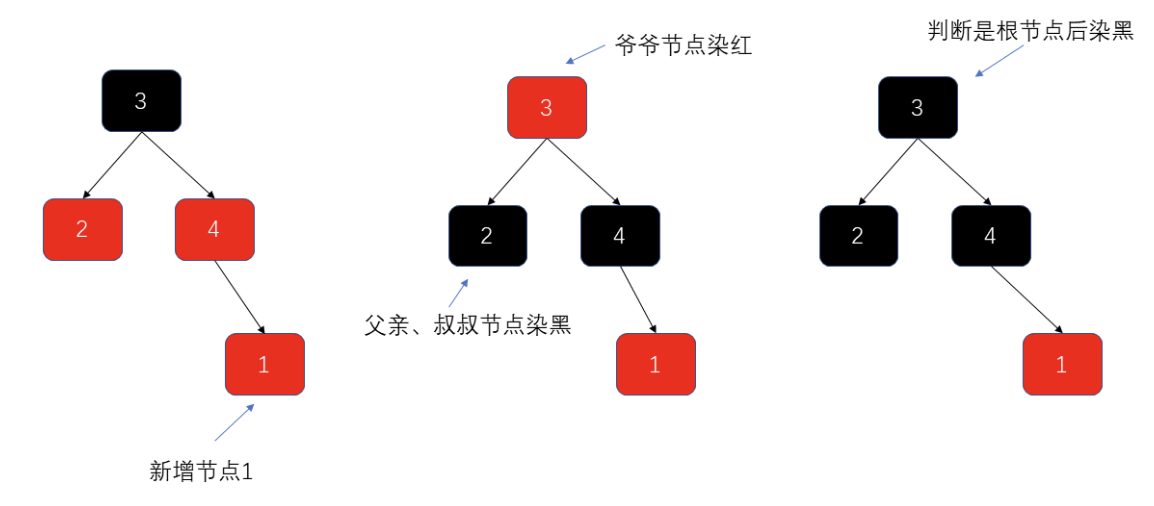
同上
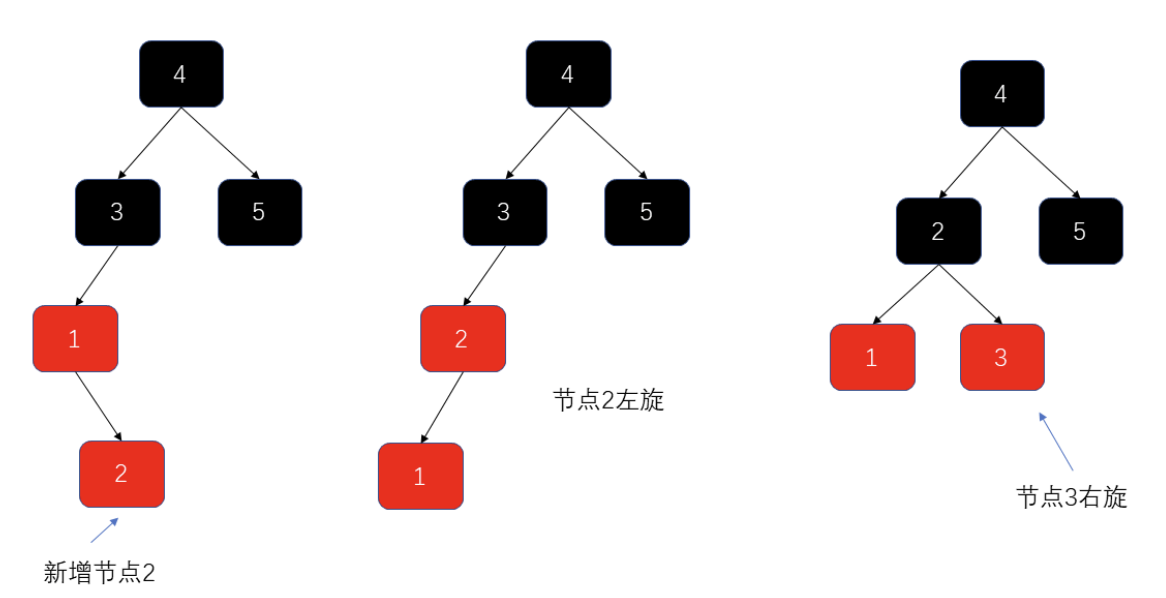
- 左旋调整
- 一次左旋
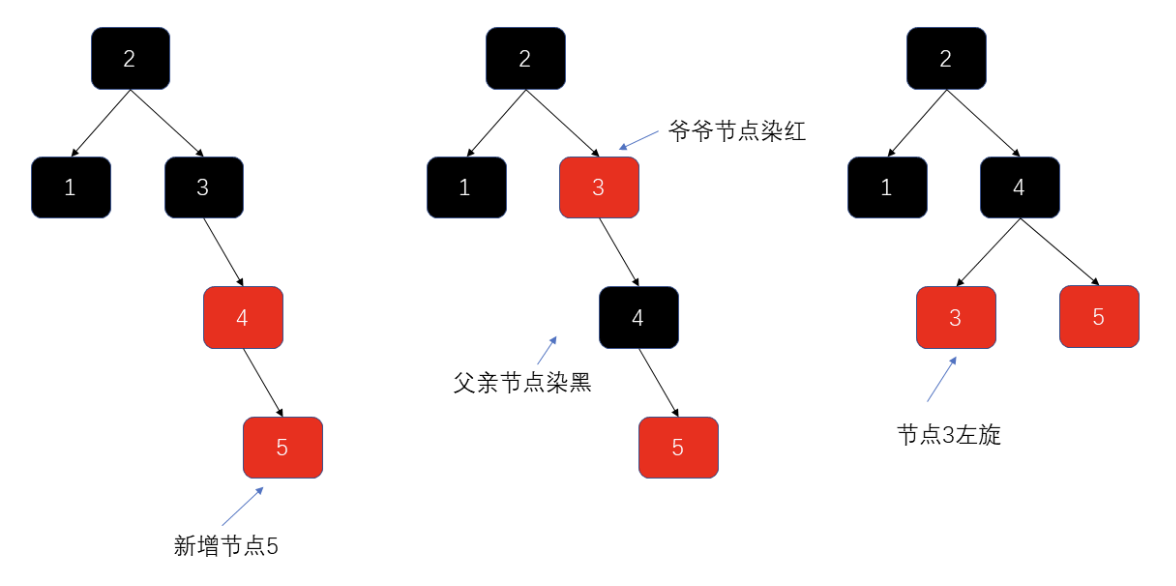
- 右旋+左旋
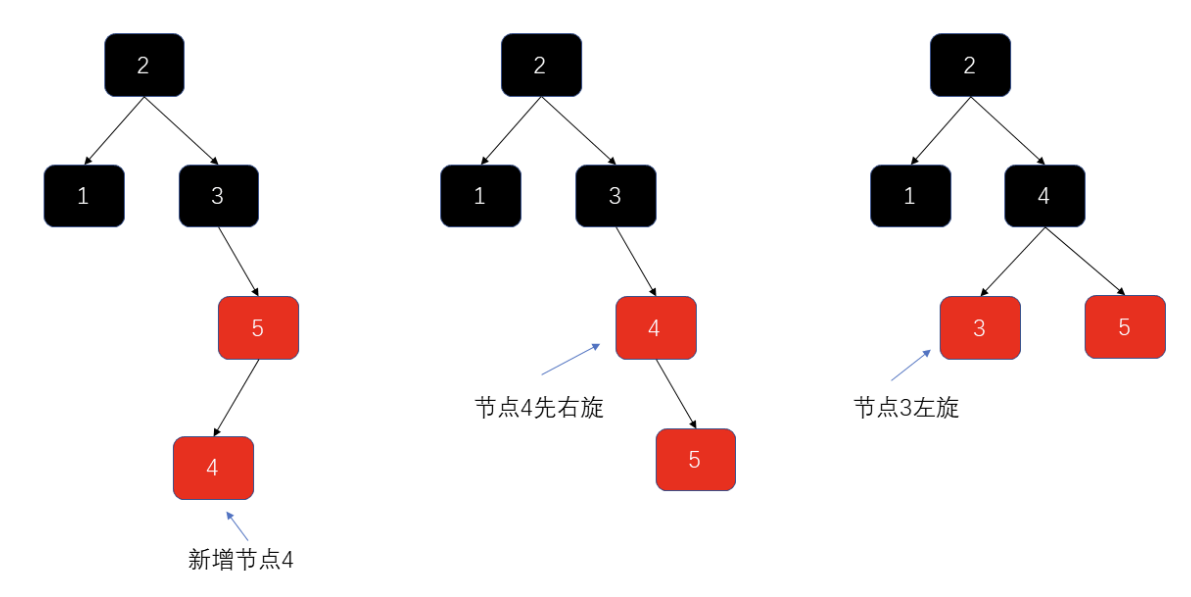
- 右旋调整
- 一次右旋
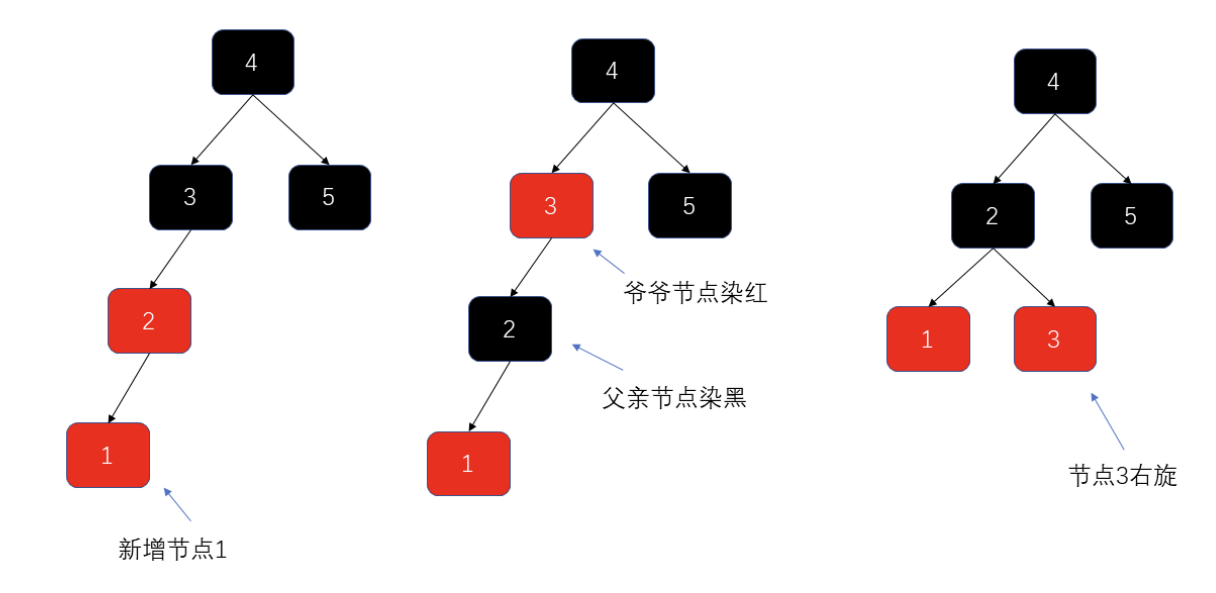
- 左旋+右旋
6 布隆过滤器
6.1 原理及使用场景
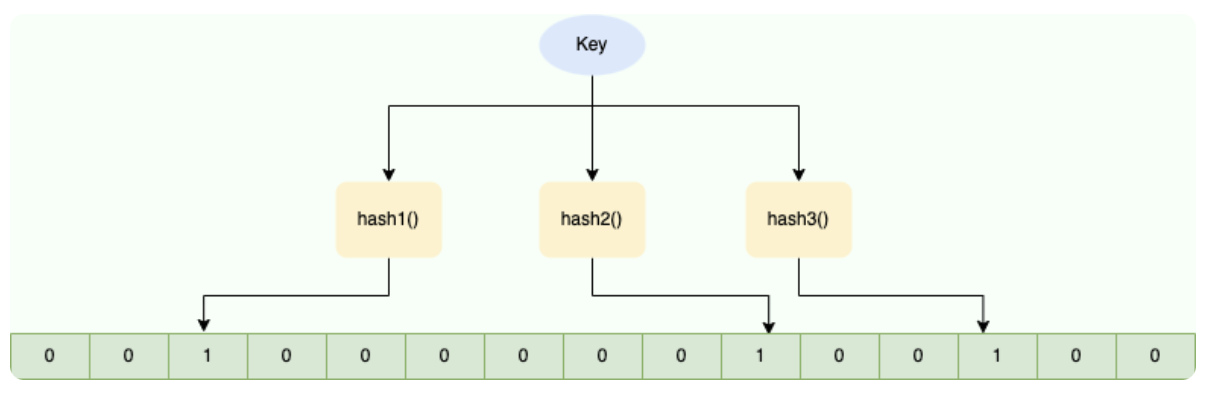
使用一个较大的bit数组保存所有数据,每个元素只占用1bit。用于判断元素是否存在,结果具有概率性,加入的元素越多,误报的概率越大。
原理:
- 当加入一个元素时:使用布隆过滤器中的哈希函数堆元素值计算,得到哈希值,根据哈希值将对应下标设置为1。
- 当判断元素是否存在时:对给定元素再次计算,如果对应位为1,则存在,否则不存在。
- 布隆过滤器说某个元素存在,小概率会误判。布隆过滤器说某个元素不在,那么这个元素一定不在。
使用场景
- 判断是否存在:防止缓存穿透、邮箱的垃圾邮件过滤,黑名单功能等
- 去重:去除以及爬取过的url,对订单号去重
6.2 编码实现
import java.util.BitSet;
public class MyBloomFilter {
private static final int DEFAULT_SIZE = 2 << 24;
private static final int[] SEEDS = new int[]{3, 13, 46, 71, 91, 134};
private BitSet bits = new BitSet(DEFAULT_SIZE);
private SimpleHash[] func = new SimpleHash[SEEDS.length];
public MyBloomFilter(){
for (int i = 0; i < SEEDS.length; i++) {
func[i] = new SimpleHash(DEFAULT_SIZE, SEEDS[i]);
}
}
public void add(Object value){
for(SimpleHash f : func){
bits.set(f.hash(value), true);
}
}
public boolean contains(Object value){
boolean ret = true;
for(SimpleHash f : func){
ret = ret && bits.get(f.hash(value));
}
return ret;
}
public static class SimpleHash {
private int cap;
private int seed;
public SimpleHash(int cap, int seed) {
this.cap = cap;
this.seed = seed;
}
public int hash(Object value) {
int h;
if (value == null) return 0;
return Math.abs(seed * (cap - 1) & ((h = value.hashCode()) ^ (h >>> 16)));
}
}
}
public static void main(String[] args) {
String value1 = "abcdefg";
String value2 = "xxxxxxx";
MyBloomFilter filter = new MyBloomFilter();
System.out.println(filter.contains(value1));
System.out.println(filter.contains(value2));
filter.add(value1);
filter.add(value2);
System.out.println(filter.contains(value1));
System.out.println(filter.contains(value2));
}